函数插值与拟合问题求解

August 6, 2025 | 数学建模, python | 10 min read

函数插值

一维插值

通俗讲就是在一维数轴上，已知n+1个数据点x_i处的函数值y_i，去寻找这个点集的近似曲线的过程。

数值计算方法

具体细节请参考《数学建模算法与应用》第三版 p114页。

多项式插值

待定系数法
拉格朗日插值法
牛顿插值法

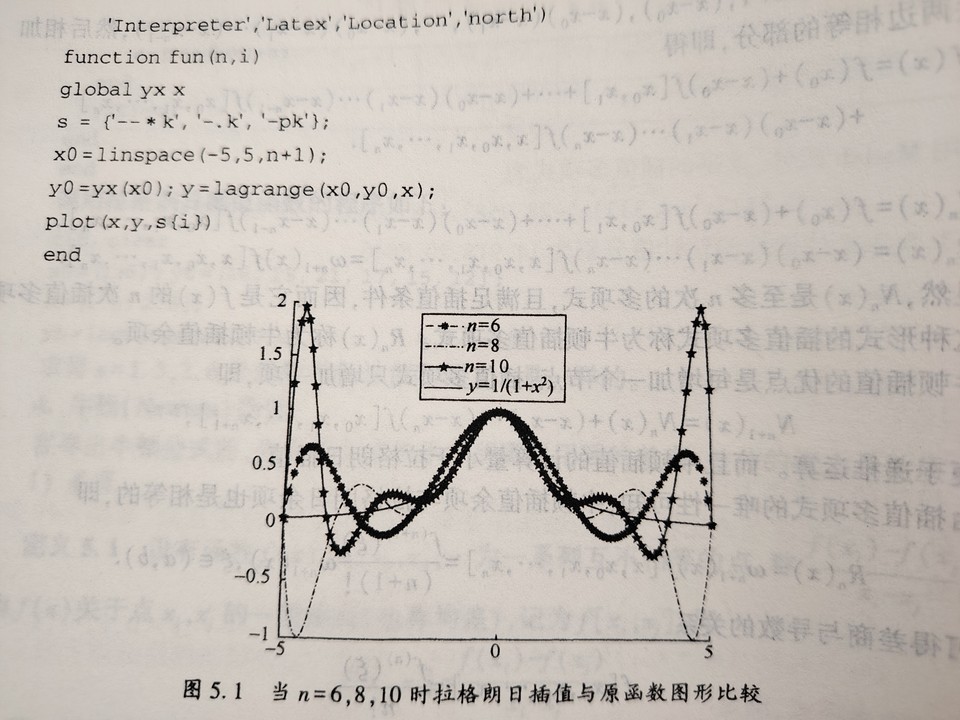
龙格震荡

上述多项式插值随着节点增多而引起的函数边缘震荡加剧的现象称为龙格震荡。

分段插值

龙格震荡问题产生的根本原因是：上述多项式方法均是尝试使用单一高次多项式来拟合所有数据点，导致剧烈震荡。

解决方法即使用分段低次多项式或局部最优的方式来构造对应曲线。

分段线性插值

当数据集足够多时，将整个插值区间分为若干个小区间，每个区间只使用2-3个点集，通过在每一个区间构造低次多项式（一次或二次函数）拟合每一个区间的曲线。

当分段足够多时，误差更小，类似极限的思想，具体过程如下：

注：缺点是：区间连接处不光滑，连接处的点集数据误差较大，实际表现则是存在不符合物理常识的“突变”。

三次样条插值

强制分段低次 + 光滑连接（三次多项式）

二维插值

二维插值的数据集给定在xOy平面上，通过求一个二元曲面函数建立数学模型。

详细过程见p121页。

scipy实现

scipy.interpolate用于解决插值问题。

使用说明

import numpy as np
from scipy.interpolate import lagrange

x: np.ndarray = np.array([0, 1, 2])
y: np.ndarray = np.array([1, 3, 2])

poly: np.poly1d = lagrange(x, y)

实现

from scipy.interpolate import lagrange, interp1d, CubicSpline
import numpy as np
import matplotlib.pyplot as plt

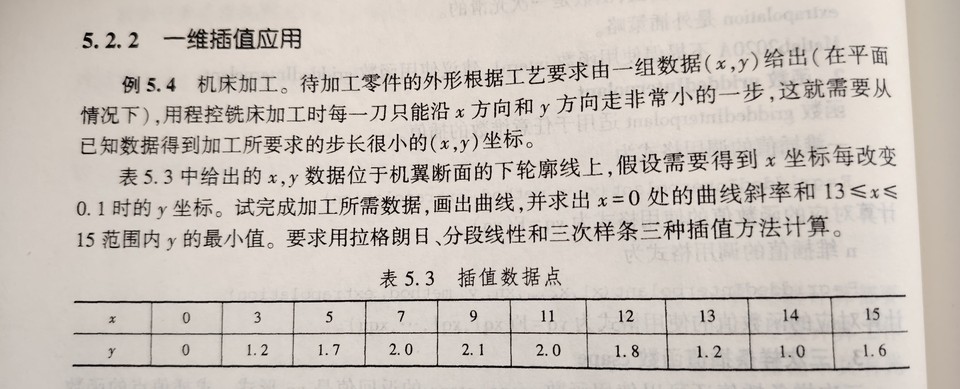
x = np.array([0, 3, 5, 7, 9, 11, 12, 13, 14, 15])
y = np.array([0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6])

#拉格朗日多项式 -> numpy.poly1d
lag_ploy = lagrange(x, y)

#生成待测x数组
x2test_arrry = np.arange(0, 15.1, 0.1)

#待测数组对应y值
y_lagrange = lag_ploy(x2test_arrry)

#拟合函数求导
derivative = np.polyder(lag_ploy)
#x=0处导数
der_of_0_lag = derivative(0)

#分段线性插值函数
interp1d_ploy = interp1d(x, y)
#y值
y_interp1d = interp1d_ploy(x2test_arrry)
#斜率
der_of_0_int = (y[1]-y[0] / (x[1]-x[0]))

#三次样条
cub_ploy = CubicSpline(x, y)

y_cubicSpline = cub_ploy(x2test_arrry)

#三次样条下0处导数
der_of_0_cub = cub_ploy.derivative(1)(0)

#第二问求最小值
mask = (x2test_arrry >= 13) & (x2test_arrry <= 15)
min_lagrange = np.min(y_lagrange[mask])
min_linear = np.min(y_interp1d[mask])
min_cub = np.min(y_cubicSpline[mask])

print("===斜率===")
print(f"拉格朗日插值在x=0处的斜率：{der_of_0_lag:.4f}")
print(f"分段线性插值在x=0处的斜率：{der_of_0_int:.4f}")
print(f"三次样条插值在x=0处的斜率：{der_of_0_cub:.4f}")

print("===最小值===")
print(f"拉格朗日插值：{min_lagrange:.4f}")
print(f"分段线性插值：{min_linear:.4f}")
print(f"三次样条插值：{min_cub:.4f}")

#绘图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
axes[0].plot(x2test_arrry, y_lagrange, label='lagrange')
axes[0].set_title('lagrange')
axes[0].set_xlabel('x')
axes[0].set_ylabel('y')
axes[0].legend()
axes[0].grid(True)

axes[1].plot(x2test_arrry, y_interp1d, label='linear')
axes[1].set_title('linear')
axes[1].set_xlabel('x')
axes[1].set_ylabel('y')
axes[1].legend()
axes[1].grid(True)

axes[2].plot(x2test_arrry, y_cubicSpline, label='cubicSpline')
axes[2].set_title('cubicSpline')
axes[2].set_xlabel('x')
axes[2].set_ylabel('y')
axes[2].legend()
axes[2].grid(True)

plt.tight_layout()
plt.show()

结果

===斜率===
拉格朗日插值在x=0处的斜率：-55.2916
分段线性插值在x=0处的斜率：1.2000
三次样条插值在x=0处的斜率：0.5023
===最小值===
拉格朗日插值：0.9391
分段线性插值：1.0000
三次样条插值：0.9828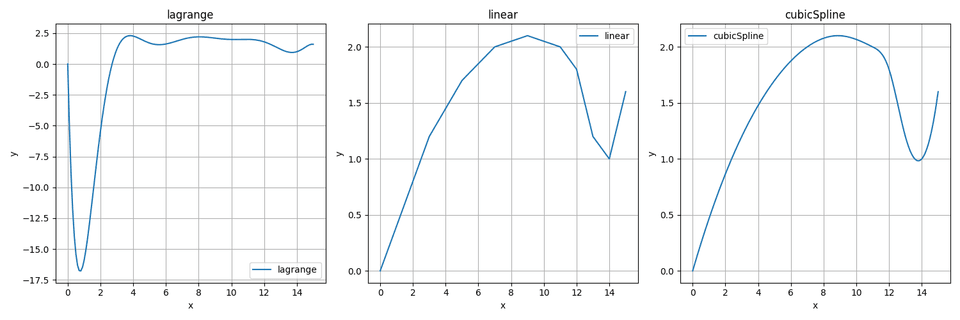

我简要简单探讨了数值方法的插值法，并基于scipy.interpolate进行了实现，使用matplotlib进行了可视化。

结果表明，拉格朗日插值法误差最大，同时Scipy官方也不推荐使用lagrange接口进行插值计算。

从图中也可知，分段线性插值的光滑性较差(x=14处)，三次样条是进行插值的最优解。

拟合问题求解

该部分对《数学建模算法与应用》第三版拟合部分涉及的线性拟合和非线性拟合问题进行python求解。

线性方程组参数拟合

问题重述

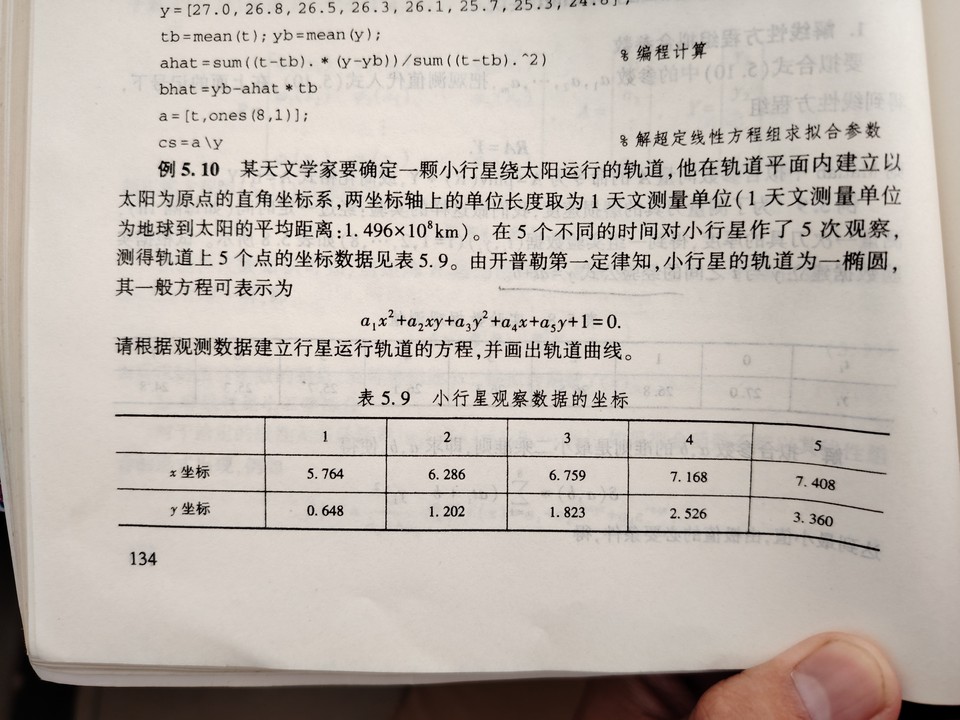
这道题需要使用高斯消元求解线性方程组的五个未知数的值，我们可以借助Numpy来实现系数矩阵的求解。

numpy.linalg.solve：要求 A 是方阵（行数 = 列数），还必须满足A 是满秩的。
numpy.linalg.lstsq：若方程不独立，则可以使用该接口实现最小二乘拟合得到近似解。

python实现

1import numpy as np
2import matplotlib.pyplot as plt
3
4x = np.array([5.764, 6.286, 6.759, 7.168, 7.408])
5y = np.array([0.648, 1.202, 1.823, 2.526, 3.360])
6
7#系数矩阵
8col1 = x**2
9col2 = x*y
10col3 = y**2
11col4 = x
12col5 = y
13
14#np.column_stack将一维数组转拼成列矩阵
15A = np.column_stack([col1, col2, col3, col4, col5])
16
17#常数矩阵b = -1
18b = -np.ones(len(x))
19
20"""
21最小二乘法求未知系数矩阵x
22np.linalg.lstsq(A, b)
23x:ndarray, residuals:ndarray 残差, rank:int 秩
24"""
25x, residuals, rank, _ = np.linalg.lstsq(A, b)
26a1, a2, a3, a4, a5 = x
27
28print(f"系数为{a1:.4f}, {a2:.4f}, {a3:.4f}, {a4:.4f}, {a5:.4f}")
29
30#表达式
31def _equation(x, y):
32    return a1 * x**2 + a2 * x * y + a3 * y**2 + a4 * x + a5 * y + 1
33
34#绘制椭圆图
35x_grid = np.linspace(3.5, 8, 1000 )
36y_grid = np.linspace(-1, 5, 1000)
37X, Y = np.meshgrid(x_grid, y_grid)
38
39Z = _equation(X, Y)
40
41#绘图
42plt.figure(figsize=(8, 6))
43plt.contour(X, Y, Z, levels=0)
44
45plt.xlabel('x')
46plt.ylabel('y')
47
48plt.show()

结果

系数为0.0508, -0.0702, 0.0381, -0.4531, 0.2643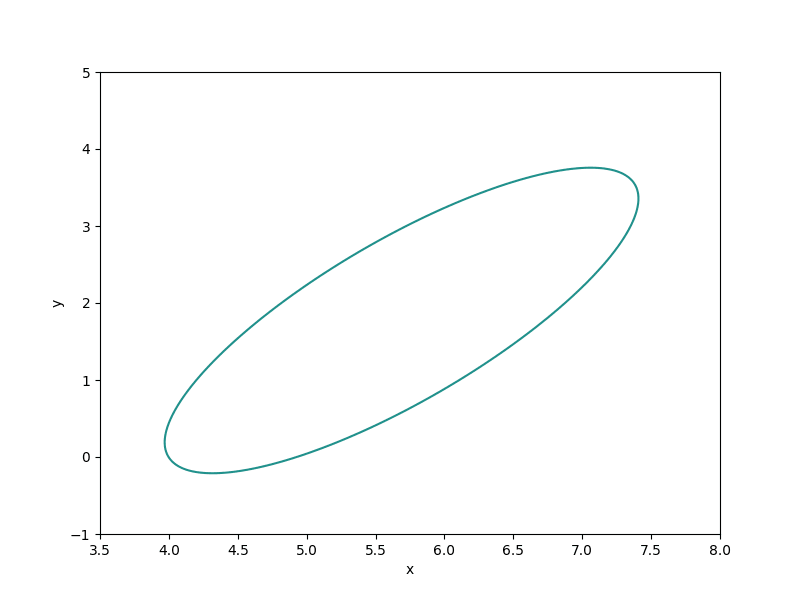

带约束的线性最小二乘拟合

问题重述

对观测数据 (x, y)，拟合函数 y = a * e^x + b * ln(x)，其中 a, b 是待求参数。约束条件：

a ≥ 0，b ≥ 0；
a + b ≤ 1。

观测数据（表 5.10）：

x = [3, 5, 6, 7, 4, 8, 5, 9]
y = [4, 9, 5, 3, 8, 5, 8, 5]

python实现

对于这一类带约束的最小二乘拟合，我们可以使用通用求解器 scipy.optimize.minimize 来求解。

1import numpy as np
2from scipy.optimize import minimize
3
4# 观测数据
5x = np.array([3, 5, 6, 7, 4, 8, 5, 9])
6y = np.array([4, 9, 5, 3, 8, 5, 8, 5])
7
8# 拟合函数
9def model(x, a, b):
10    return a * np.exp(x) + b * np.log(x)
11
12# 目标函数（最小化残差平方和）
13def objective(params, x, y):
14    a, b = params
15    return np.sum((y - model(x, a, b)) ** 2)
16
17# 初始参数估计
18initial_guess = [0, 0]
19
20# 变量边界约束 a >= 0, b >= 0
21bounds = [(0, np.inf), (0, np.inf)]
22
23# 额外约束 a + b <= 1
24def constraint(params):
25    a, b = params
26    return 1 - (a + b)
27
28constraints = [{'type': 'ineq', 'fun': constraint}]
29
30# minimize 求解最小化问题（也用来实现规划问题）
31result = minimize(objective, initial_guess, args=(x, y), bounds=bounds, constraints=constraints)
32
33a, b = result.x
34print(f"a = {a:.4f}, b = {b:.4f}")

结果

a = 0.0005, b = 0.9995

非线性最小二乘拟合

Q1

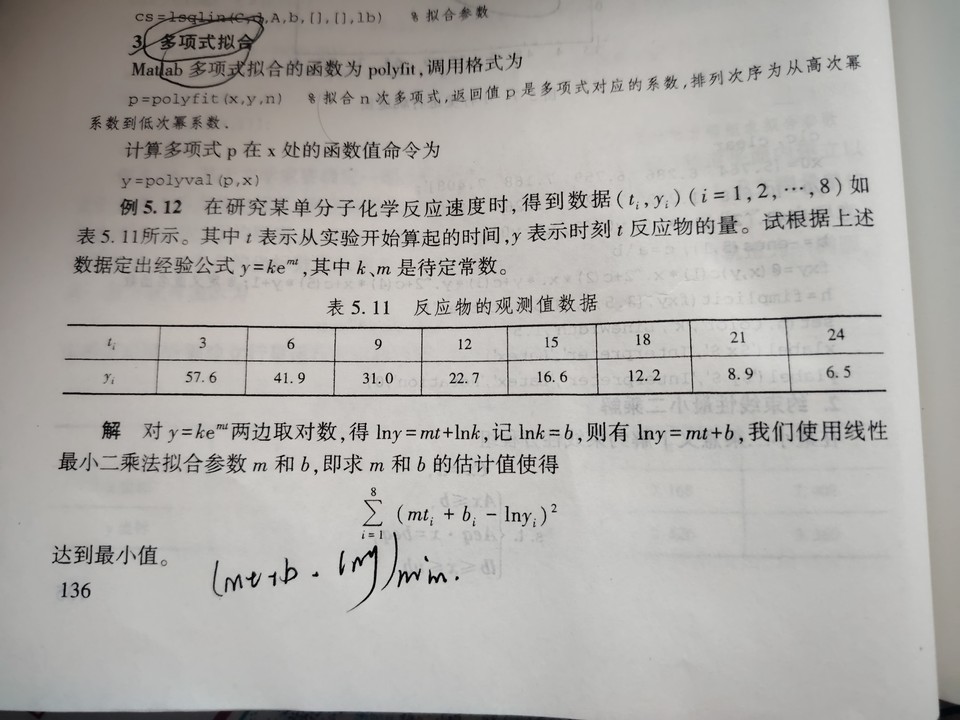
实现

对于某些非线性拟合，可以先进行数学运算：通过对两边取对数，转化为线性最小二乘使用 np.linalg.lstsq 进行拟合求解。

import numpy as np

t = np.arange(3, 27, 3)
y = np.array([57.6, 41.9, 31.0, 22.7, 16.6, 12.2, 8.9, 6.5])

ln_y = np.log(y)

A = np.column_stack([t, np.ones_like(t)])

parmas, _, _, _ = np.linalg.lstsq(A, ln_y)

m, b = parmas
k = np.exp(b)

print(f"m = {m:.4f} \nb = {b:.4f} \nk = {k:.4f}")

结果

m = -0.1037 
b = 4.3640 
k = 78.5700

Q2

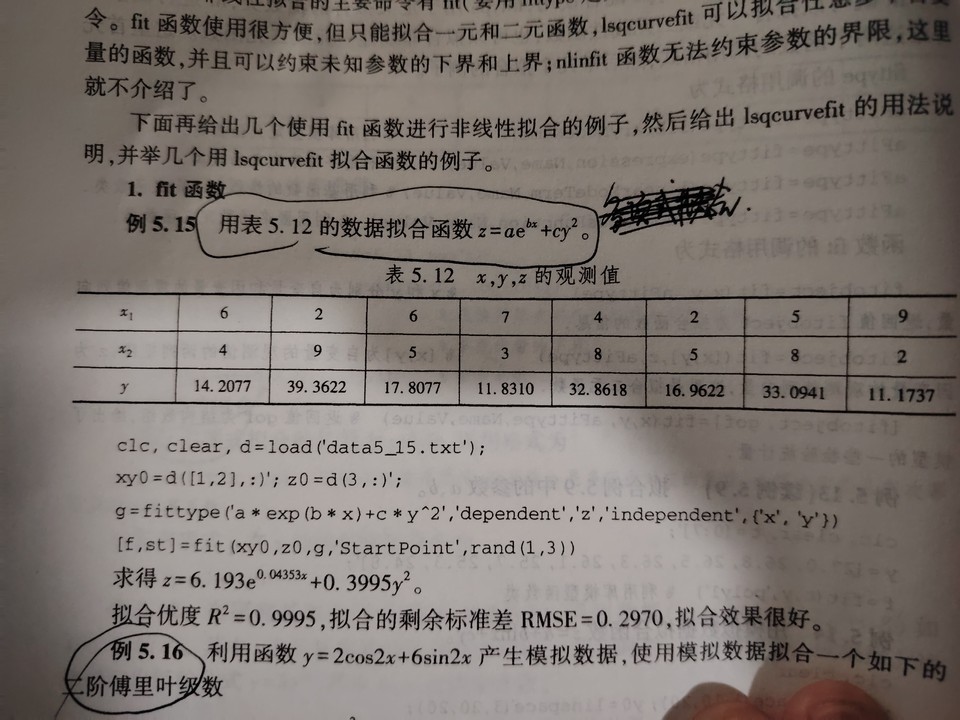
对于非线性拟合，我们也可以直接选用 scipy.optimize.curve_fit 进行求解，具体参数说明请查看官方文档。

python实现

1import numpy as np
2from scipy.optimize import curve_fit
3
4x = np.array([6, 2, 6, 7, 4, 2, 5, 9])
5y = np.array([4, 9, 5, 3, 8, 5, 8, 2])
6z = np.array([14.2077, 39.3622, 17.8077, 11.8310, 32.8618, 16.9622,  33.0941, 11.1737])
7
8def _objective(parmas, a, b, c):
9    x, y = parmas
10    return a * np.exp(b * x) + c * y ** 2
11
12parmas = (x, y)
13
14popt, _ = curve_fit(_objective, parmas, z)
15a, b, c = popt
16
17print(f"a={a:.4f}\nb={b:.4f}\nc={c:.4f}")

结果

a=6.1929
b=0.0435
c=0.3995

Q3

问题重述

1import numpy as np
2import matplotlib.pyplot as plt
3from scipy.optimize import curve_fit
4
5x = np.linspace(-5, 5, 50)
6y = np.linspace(-5, 5, 50)
7X, Y = np.meshgrid(x, y)  # 二维网格,所有组合
8xy_flat = np.column_stack((X.ravel(), Y.ravel())) 
9
10def _function(xy, u1, u2, u3):
11    x = xy[:, 0]  # 提取所有样本的x
12    y = xy[:, 1]
13    return np.exp(-((x - u1) ** 2 + (y - u2) ** 2) / (2 * u3 ** 2))
14
15z_real = _function(xy_flat, 1, 4, 6)
16
17#加入噪声
18z_noise = z_real + 0.05 * np.random.normal(size=z_real.shape)
19
20predit = [0, 0, 1]
21
22popt, _ = curve_fit(_function, xy_flat, z_noise, p0=predit)
23u1, u2, u3 = popt
24
25print("真实值：u1=1, u2=4, u3=6")
26print(f"拟合数据：u1={u1:.4f}, u2={u2:.4f}, u3={u3:.4f}")

绘图

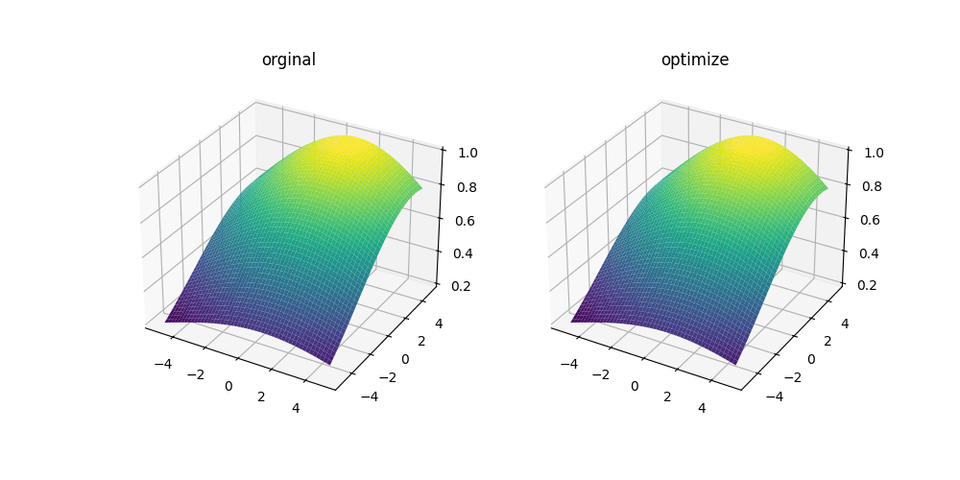
fig = plt.figure(figsize=(10,5))
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(X, Y, z_real.reshape(X.shape), cmap='viridis')
ax1.set_title("orginal")  

ax2 = fig.add_subplot(122, projection='3d')
ax2.plot_surface(X, Y, _function(xy_flat, *popt).reshape(X.shape), cmap='viridis')  
ax2.set_title("optimize")
plt.show()

结果

真实值：u1=1, u2=4, u3=6
拟合数据：u1=1.0127, u2=3.9832, u3=5.9700

原函数曲面及拟合曲面图形：